Pythonで標準化
標準化が難しい!
標準化の概念がめちゃくちゃ難しいです。感覚的に理解できません。
ということで、色々と手を動かして標準化がどういうものなのか見ていきたいと思います。
人間の年齢(age)と身長(tall)をデータにして見ていきます。
カッコ良いので数式のプラグイン『MathJax-LaTeX』を入れてみました。
$$x = age(年齢) y = tall(身長)$$Sampleデータを取り込む
まずは、データをそのまま表示します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
a = np.random.randint(10,80,100)
a = pd.Series(a,name="age")
b = np.random.randint(120,190,100)
b = pd.Series(b,name="tall")
df = pd.concat([a,b], axis=1)
# age tall
# 0 44 121
# 1 64 154
# 2 20 145
# 3 71 140
df.plot(x="age",y="tall",kind='scatter') # 散布図で表示
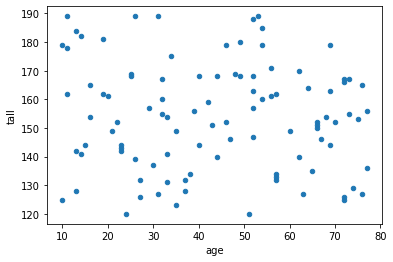
とりあえず、標準化してみる
標準化とは標準偏差で割り算することのようですので、やってみます。
df.mean() # 平均値
# age 49.86
# tall 153.27
df.std() # 標準偏差
# age 19.041168
# tall 21.451781
df_mean_std = (df - df.mean())/ df.std()
df_mean_std.plot(x="age",y="tall",kind='scatter') # 散布図で表示
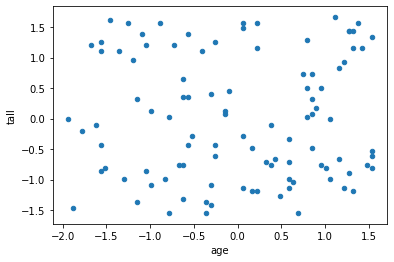
そして、標準化したデータの標準偏差を求めると・・・
df_mean_std.std()
# age 1.0
# tall 1.0
X軸、y軸ともに標準偏差が "1" となっています。
分かりやすく言い換えると、データの標準化とは、もともとは単位の異なるデータだったものを、『平均値からのバラつき具合』という同じ尺度(標準偏差 "1")に変換することを指します。
数式で標準偏差を考えてみる
それでは、最後に数式でも考えてみることにしましょう。
分散を求める数式は以下になります。
$$σ^2 = \frac{1}{n}\sum_{n=1}^n(x_i-\overline{x})^2$$分散と標準偏差は以下のような関係になります。
$$σ^2 = 分散 σ = 標準偏差$$標準化の計算手順
上記の分散を求める式の両辺を\(σ^2\)で割り算するとこのようになります。
$$1 = \frac{1}{n}\sum_{n=1}^n(\frac{x_i-\overline{x}}{σ})^2$$標準化を数式で表す場合、左辺を "1" にするということだったのですね。
そして、この数式を言い換えれば、標準化の計算方法はデータから平均値を引いて標準偏差で割る、となりますね。
$$\frac{x_i-\overline{x}}{σ}$$さて、分かったような分からないような・・・。いつかきっと分かりますように!