Python で正規化
正規化をやってみよう
以前の記事「Pythonで標準化」の続きのような感じですが、Pythonで正規化をやってみます。
まずは、必要なモジュールを読み込んでデータを用意しましょう。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
a = np.random.randint(0,100,100)
a = pd.Series(a,name="a_score")
b = np.random.randint(100000,1000000,100)
b = pd.Series(b,name="b_score")
df = pd.concat([a,b], axis=1)
print(df)
# a_score b_score
# 0 8 483168
# 1 33 162257
# 2 64 253630
# 3 35 280976
df.plot(x="a_score",y="b_score",kind='scatter') # 散布図で表示
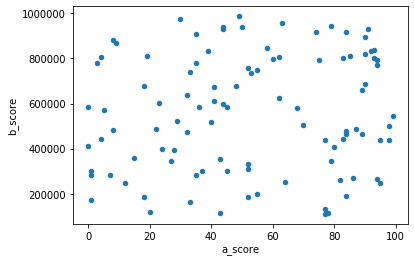
正規化の数式
それでは、正規化の数式を見てみましょう。
$$x' = \frac{x - \min{\left( x \right)}}{\max{\left( x \right)} - \min{\left( x \right)}}$$数式そのものは、そこまで難しくないですね。最大値と最小値を使って簡単に表現できます。
実際に計算してみましょう。
df_min = df.min()
print(df_min)
# a_score 0
# b_score 110498
df_max = df.max()
print(df_max)
# a_score 99
# b_score 987037
df_nomal = (df - df_min) / (df_max - df_min)
print(df_nomal)
# a_score b_score
# 0 0.080808 0.425161
# 1 0.333333 0.059049
# 2 0.646465 0.163292
# 3 0.353535 0.194490
df_nomal.plot(x="a_score",y="b_score",kind='scatter') # 散布図で表示
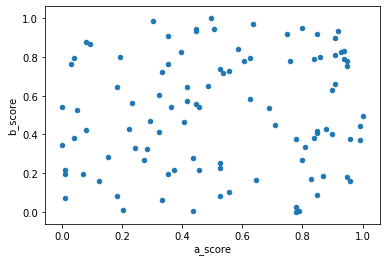
検算してみる
"a_score" の index=1 の 0.333333 が正しいか検算します。
$$\frac{x - \min{\left( x \right)}}{\max{\left( x \right)} - \min{\left( x \right)}} = \frac{33 - 0}{99 - 0} = \frac{33}{99} = 0.333333...$$"b_score" の index=2 の 0.163292 が正しいか検算します。
$$\frac{x - \min{\left( x \right)}}{\max{\left( x \right)} - \min{\left( x \right)}} = \frac{253630 - 110498}{987037 - 110498} = \frac{143132}{876539} = 0.163292...$$当たり前の結果ですが、計算結果は正しかったですね。
何となくわかった気がする
ここまでやってみて、何となくわかったような気がしています。
正規化は0~1に数字を置き換える。散布図で見ると、点の位置が変わっているわけではない。
標準化は標準偏差が1になる。散布図で見ると、平均値を0として、距離で点が表現されるため、位置が変わる。